MINERÁL.CZ

2. Strukturní a chemická krystalografie

2.1. Struktura krystalu a prostorová mřížka

Na obr. 1 je znázorněn krystal alfa-polonia, jehož jednotlivé atomy jsou zde zobrazeny jako koule. Z tohoto obrázku je zřejmé, že vnitřní stavba krystalických látek je podmíněna určitým řádem - libovolně zvolený atom Po se pravidelně opakuje ve třech směrech X, Y a Z, přičemž dva sousední atomy jsou od sebe vzdáleny vždy o konstantní vzdálenost. V této struktuře představuje atom polonia základní motiv, jehož pravidelným opakováním se vytváří trojrozměrná krystalová struktura.

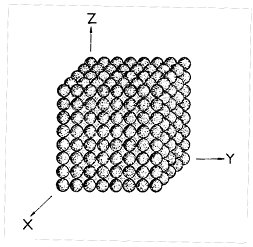
Obr. 1. Krystalová struktura alfa-polonia.

Výběr základního motivu není vždy tak jednoduchý a jednoznačný jako u krystalové struktury alfa-polonia, kde jej tvoří pouze jediný atom. Na obr. 2a je znázorněna složitější struktura (pro přehlednost pouze dvojrozměrně). Základní motiv této struktury musí obsahovat již čtyři atomy a lze jej zvolit několika způsoby, z nichž dva jsou znázorněny na obr. 2a - pravidelným opakováním prvního nebo druhého základního motivu ve směru os X a Y lze postupně vytvořit celou na obrázku znázorněnou strukturu.

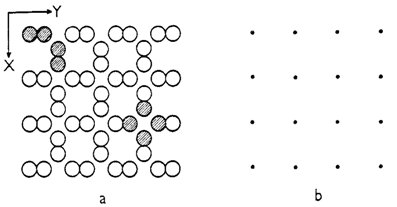
Obr. 2. Krystalová struktura a dvojí výběr základního motivu (a)
a znázorněné krystalové struktuře odpovídající mřížka (b).

Obecně lze v libovolné krystalové struktuře vymezit základní motiv, což je vlastně seskupení nejmenšího počtu stavebních jednotek (atomů, iontů), jehož periodickým opakováním ve třech směrech lze vytvořit krystalovou strukturu. Pokud chceme vyjádřit geometrii krystalové struktury jako celku, nahradíme základní motiv jediným bodem. Tento bod se bude v prostoru periodicky opakovat a vytvoří tao množinu bodů, která se označuje jako prostorová mřížka (nebo jen jako mřížka). Je zřejmé, že takto odvozená prostorová mřížka zachovává původní geometrické vztahy v krystalové struktuře. Každý bod prostorové mřížky (zvaný též mřížkový bod nebo uzel) má stejné a stejně orientované okolí a vůbec nezáleží na tom, jaká je pozice uzlu vůči základnímu motivu; je však nezbytné, aby tato pozice byla u všech uzlů stejná.

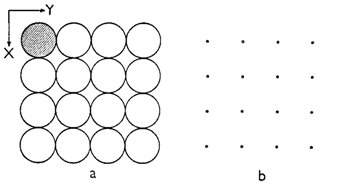
Obr. 3. Projekce struktury alfa-Po do roviny XY (a) a odpovídající mřížka (b).

Na obr. 3a je znázorněna projekce struktury alfa-Po do roviny XY. Odpovídající mřížka, v níž každý mřížkový bod reprezentuje jeden atom polonia, je znázorněna na obr. 3b. Geometrii o něco komplikovanější krystalové struktury na obr. 2a lze vyjádřit mřížkou, která je znázorněna na obr. 2b (volba strukturního motivu nemá žádný vliv na rozměry a orientaci mřížky). Porovnáním mřížek na obr. 2b a 3b, které vyjadřují geometrii dvou výrazně odlišných krystalových struktur, zjišťujeme, že obě mřížky jsou téměř totožné a že tedy jde o mřížky téhož typu. Z toho plyne obecně platný závěr: Každá krystalová struktura má pouze jednu vlastní mřížku, ale dvě navzájem odlišné krystalové struktury mohou mít mřížku stejného typu. Je nutno zdůraznit, že krystalová struktura představuje určitou fyzikální realitu (tedy existuje), zatímco mřížka je pouze pomůckou, která slouží k popisu krystalové struktury. Ne ve skutečnosti, ale pouze v abstrakci lze krystalovou strukturu rozložit na mřížku a základní motiv (nebo obráceně: z mřížky a základního motivu lze vytvořit krystalovou strukturu).

2.2. Základní buňka

Protože v každé mřížce se uzly pravidelně opakují, lze celou mřížku odvodit z libovolného uzlu, který si zvolíme za počátek mřížky. Mřížku získáme postupným posunováním (translací) tohoto uzlu ve třech nekomplanárních směrech (tj. směrech neležících v jedné rovině) pomocí trojice translačních vektorů. Na obr. 4 je znázorněna mřížka, z jejíhož libovolného uzlu můžeme vést řadu translačních vektorů - sedm translačních vektorů je na obrázku znázorněno, avšak pro jednoznačný popis dané mřížky stačí vybrat pouze tři vektory neležící v jedné rovině. Tato trojice vektorů určuje rovnoběžnostěn, jenž se nazývá základní buňka. Délky hran základní buňky označujeme jako a ₀ , b ₀ a c ₀ a jimi sevřené úhly jako alfa, beta a gama (přičemž úhel alfa leží mezi hranami b ₀ a c ₀ , úhel beta mezi a ₀ a c ₀ , úhel gama mezi a ₀ a b ₀ ). Hodnoty a ₀ , b ₀ , c ₀ , alfa, beta a gama se označují jako mřížkové parametry (případně parametry základní buňky). Obr. 5 naznačuje, že zobrazenou mřížku by snad bylo možno popsat pomocí různě zvolených buněk. Není tomu tak, neboť při výběru buňky vhodné pro konkrétní mřížku (a tedy krystalovou strukturu) je nutno respektovat tato pravidla:

• 1. Základní buňka musí mít stejnou souměrnost jako celá struktura.
• 2. Počet stejných hran a úhlů mezi hranami zvolené základní buňky musí být maximální.
• 3. Počet pravých úhlů v buňce musí být maximální.
• 4. Při splnění předcházejících požadavků musí být objem základní buňky co nejmenší.

Ze tří na obr. 5 znázorněných základních buněk tedy zvolíme tu prostřední.

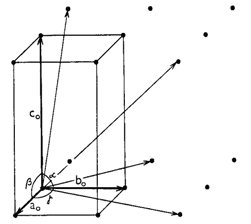
Obr. 4. Část množiny základních translačních vektorů v mřížce a základní buňka..

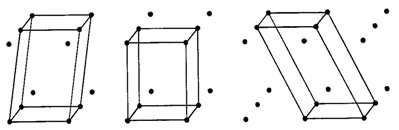
Obr. 5. Volba buněk v mřížce.

Základní buňky můžeme rozdělit podle toho, kolik uzlů připadá na jejich objem. Primitivní buňka obsahuje uzly pouze ve svých osmi vrcholech, přičemž každý z těchto uzlů jí patří jednou osminou, neboť každý z uzlů je společný pro 8 sousedních buněk. Na objem primitivní buňky tedy připadá pouze jeden uzel. Tělesně (prostorově) centrovaná buňka obsahuje kromě osmi uzlů ve vrcholech ještě jeden uzel v průsečíku tělesových úhlopříček - na objem tělesně centrované buňky tedy připadají 2 uzly. Bočně (bazálně) centrovaná buňka je kromě osmi uzlů ve vrcholech tvořena další dvojicí uzlů, které leží ve středu dvou protilehlých stěn, přičemž každý z uzlů této dvojice náleží současně dvěma buňkám - na objem bočně centrované buňky tedy připadají opět 2 uzly. Plošně centrovaná buňka je tvořena osmi uzly ve vrcholech a šesti uzly ve středech všech šesti stěn - na objem plošně centrované buňky tedy připadají 4 uzly.

Jak již bylo uvedeno, je znám obrovský počet odlišných krystalových struktur, z nichž každá má svou vlastní mřížku, v níž lze za použití výše uvedených pravidel zvolit vhodnou základní buňku. Existuje však pouze 14 typů strukturních mřížek, jimž odpovídá 14 základních buněk, označovaných jako Bravaisovy buňky. Na obr. 6 je znázorněno všech čtrnáct Bravaisových buněk, které jsou na základě své souměrnosti rozděleny do 7 krystalových soustav (primitivní buňky jsou označeny písmenem P nebo R, tělesně centrované písmenem I, bočně centrované písmenem C a plošně centrované písmenem F).

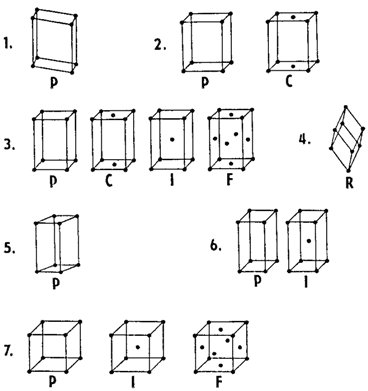
Obr. 6. Čtrnáct Bravaisových buněk: 1 - triklinická soustava, 2 - monoklinická soustava, 3 - rombická soustava, 4 - trigonální soustava, 5 - hexagonální soustava, 6 - tetragonální soustava, 7 - kubická soustava. Primitivní buňka trigonální soustavy je označena písmenem R (jde o tzv. romboedrickou buňku), primitivní buňky ostatních soustav jsou označeny písmenem P; prostorově centrované buňky jsou označeny písmenem I, bočně centrované buňky písmenem C a plošně centrované buňky písmenem F.

Symetrie prostorových mřížek a následně Bravaisových buněk má vliv na hodnoty některých mřížkových parametrů a na vztahy mezi nimi. U jednotlivých krystalových soustav je situace následující:

• triklinická soustava: a ₀ , b ₀ , c ₀ , alfa, gama a beta jsou libovolné;
• monoklinická soustava - existují dvě možnosti:
• a/ alfa=beta=90°; gama, a ₀ , b ₀ a c ₀ jsou libovolné;
• b/ alfa=gama=90°; beta , a ₀ , b ₀ a c ₀ jsou libovolné;
• rombická soustava: alfa=gama=beta=90°; a ₀ , b ₀ a c ₀ jsou libovolné;
• tetragonální soustava: alfa=gama=beta=90°; a ₀ =b ₀ ; c ₀ je libovolné;
• trigonální soustava: alfa=gama=beta  90°; a ₀ =b ₀ =c ₀ ;
• hexagonální soustava: alfa=gama=90°; beta=120°; a ₀ =b ₀ ; c ₀ je libovolné;
• kubická soustava: alfa=gama=beta = 90°; a ₀ =b ₀ =c ₀ .

K vyjádření geometrie triklinické mřížky je tedy nutno uvést hodnoty všech mřížkových parametrů - např. chalkantit (modrá skalice) má a ₀ =6,12, b ₀ =10,69, c ₀ =5,96 (tyto hodnoty jsou uvedeny v Å, přičemž 1Å=1 x 10-10 m), alfa=97°35’, gama=107°10’ a beta=77°33’. Například u látek krystalujících v soustavě rombické stačí k vyjádření geometrie příslušného typu Bravaisovy mřížky uvést hodnoty a ₀ , b ₀ a c ₀ , neboť hodnoty úhlů alfa, gama a beta jsou dány rombickou soustavou - např. rombická modifikace síry (označovaná jako alfa-S) má a ₀ =10,44, b ₀ =12,84 a c ₀ =24,37. V případě látek krystalujících v kubické soustavě se uvádí pouze hodnota a ₀ - např. u diamantu a ₀ =3,57.

Délky hran základní buňky se dosud často uvádějí (a tak je tomu i v těchto skriptech) v ångströmech (Å). V soustavě SI není používání této jednotky povoleno a délky hran základní buňky by měly být udávány v nanometrech, přičemž 1 nm=1 x 10-9 m (1 nm=10 Å).

Mřížkové parametry se někdy nesprávně označují jako mřížkové konstanty. Tento termín je však nevhodný, neboť velikost mřížkových parametrů závisí na teplotě, tlaku, ale též na chemickém složení daného minerálu.

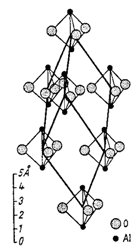
Obr. 7. Krystalová struktura korundu.

Obr. 7 schematicky znázorňuje krystalovou strukturu korundu. Je to minerál o vzorci Al2O3, jenž krystaluje v soustavě trigonální. Základní motiv korundu je tvořen molekulou Al2O3. Rozložení těchto molekul v krystalové struktuře určuje geometrii základní buňky, která je na obrázku pro přehlednost znázorněna jen neúplně (je zobrazeno pouze 7 uzlů - tomu odpovídá 9 vyznačených hran buňky z celkového počtu 12); uzel základní buňky je umístěn vždy v centru znázorněných základních motivů.

Na obr. 8 je schematicky znázorněna základní buňka chalkopyritu (CuFeS2), jenž má primitivní tetragonální buňku. Na objem základní buňky tohoto minerálu připadají 4 atomy Cu, 4 atomy Fe a 8 atomů S, což znamená, že na objem základní buňky připadají 4 vzorcové jednotky (4 x CuFeS2). Počet vzorcových jednotek v základní buňce se zpravidla označuje písmenem Z (v případě chalkopyritu Z=4).

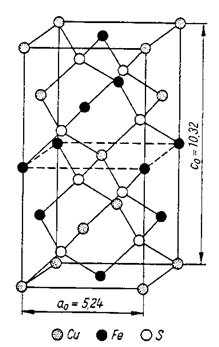
Obr. 8. Základní buňka chalkopyritu

2.3. Reálné krystalové struktury

Až dosud jsme předpokládali, že krystalová struktura je ideálně periodická a že se její základní motiv periodicky opakuje. Takovou ideální strukturu by měl pouze ideální, nekonečně velký krystal, který ve skutečnosti neexistuje. Význam idealizované představy krystalu spočívá v tom, že pomocí ideální krystalové struktury jsme schopni definovat skutečnou (reálnou) krystalovou strukturu. Reálná krystalová struktura je ve srovnání se svým ideálním vzorem vždy určitým způsobem více či méně porušena. Za poruchu ideální krystalové struktury považujeme každou (i zcela nepatrnou) odchylku od dokonalé periodičnosti.

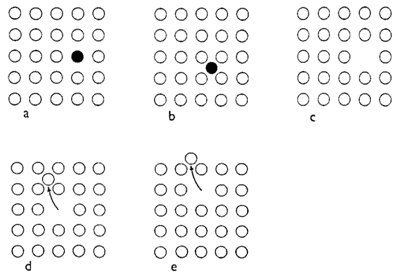
Obr. 9. Bodové poruchy ve struktuře reálných krystalů: nahrazení atomu neboli substituce (a), umístění atomu v intersticiální poloze (b), vakance (c), Frenkelova porucha (d) a Schottkyho porucha (e).

Existuje celá řada typů poruch ideální krystalové struktury, z nichž nejběžnější jsou bodové poruchy a dislokace. Bodové poruchy různých typů znázorňuje obr. 9. V reálné krystalové struktuře je vždy přítomen určitý počet cizích atomů (nevyjádřených v idealizovaném chemickém vzorci minerálu), které zaujímají polohy, jež jsou v ideální krystalové struktuře vyhrazené jiným atomům. Uvedené nahrazování či zastupování se označuje jako substituce a je schematicky znázorněno na obr. 9a - protože substituce je velmi rozšířeným jevem a z hlediska mineralogie je neobyčejně významná, bude detailně vyložena v kapitole 2.4. Ideální krystalová struktura je narušována i přítomností atomů v tzv. intersticiálních (vmezeřených) polohách (obr. 9b) nebo vakancemi, tj. neobsazenými atomovými polohami v krystalové struktuře (obr. 9c). Při tepelných vibracích struktury se atom může ze své rovnovážné polohy vychýlit natolik, že zůstane v intersticiální poloze a zanechá po sobě vakanci - tato kombinace intersticiálního atomu s vakancí se označuje jako Frenkelova porucha (obr. 9d); obdobně vzniká Schottkyho porucha (obr. 9e), při níž však atom vystoupí až na povrch krystalu. Je pochopitelné, že bodové poruchy se ve svém okolí projevují vždy určitou deformací krystalové struktury (v porovnání s ideální strukturou). Dislokace jsou v podstatě dvou základních typů: jde o hranové a šroubové dislokace, jejichž charakter a možný způsob vzniku je zřejmý z obr. 10.

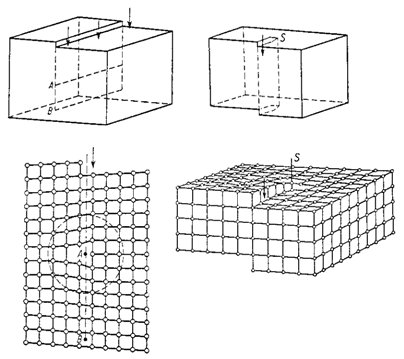
Obr. 10. Hranová dislokace (vlevo) a šroubová dislokace (vpravo). V dolní polovině obrázku jsou znázorněny mřížky porušené těmito dislokacemi, v horní polovině jsou znázorněny mechanické modely vzniku dislokací.

Uvedené poruchy a jejich vzájemné kombinace často způsobují mozaikovou stavbu krystalických látek. V krystalové struktuře těchto látek lze rozlišit jednotlivé oblasti s víceméně ideální stavbou (tzv. bloky), které jsou vůči sobě navzájem poněkud posunuty (obr. 11a); někdy lze mozaikovou (blokovou) stavbu krystalů pozorovat i makroskopicky (na obr. 11b je znázorněn krystal pyritu s velmi výraznou blokovou stavbou). Defekty v krystalové struktuře se mohou projevit např. i přítomností tzv. „štěrbin“, tj. prázných dutin zpravidla ploše čočkovitého tvaru, které sahají od povrchu krystalu do určité hloubky. Defekty v krystalové struktuře významně ovlivňují procesy růstu krystalů (kapitola 4.2).

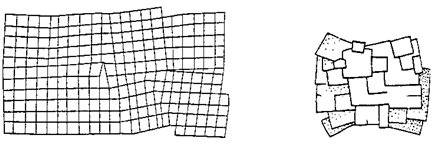
Obr. 11. Schéma mozaikové stavby krystalu (vlevo); mozaiková stavba pyritu (vpravo).

2.4. Zastupování atomů v krystalové struktuře

Mnoho minerálů má proměnlivé chemické složení. Zastupování jednoho elementu druhým ve struktuře minerálu je spíše pravidlem než výjimkou. Krystalické látky, v jejichž struktuře k tomuto zastupování dochází, jsou někdy označovány jako pevné roztoky nebo také jako směsné krystaly. Tyto termíny odpovídají původním představám, podle nichž proměnlivé chemické složení minerálů souvisí s tím, že v jediném homogenním krystalu jsou přítomny molekuly dvou nebo více sloučenin. Tak například olivín byl považován za směs dvou hlavních složek: forsteritu Mg ₂ [SiO ₄ ] a fayalitu Fe ₂ [SiO ₄ ]. Složení v přírodě rozšířených olivínů lze vyjádřit vzorcem (Mg,Fe) ₂ [SiO ₄ ], přičemž z takto uvedeného vzorce není zřejmý poměr mezi Mg a Fe. Pokud přesně známe chemické složení určitého olivínu, lze k vyjádření jeho chemismu užít krystalochemického vzorce, z něhož již bude poměr mezi Mg a Fe zřejmý (způsob výpočtu krystalochemických vzorců je uveden v následující stati).

Termíny „pevný roztok“ a „směsný krystal“ se v mineralogii stále používají velmi často, i když v iontové struktuře minerálů nejsou jednotlivé molekuly přítomny. Strukturu těchto minerálů je možno považovat za teoreticky nekonečnou trojrozměrnou strukturu, v níž se jednotlivé ionty zastupují v ekvivalentních pozicích bez podstatných deformací této struktury.

Hlavním faktorem, jenž určuje, zda se dva prvky nebo ionty mohou ve struktuře minerálu vzájemně zastupovat, je jejich velikost. Zastupující se ionty nemusí mít stejnou valenci nebo náboj, neboť elektroneutrality může být dosaženo dalším souběžným zastupováním v téže struktuře (jde o tzv. sdruženou substituci). Například v řadě „pevných roztoků“ mezi albitem Na[AlSi ₃ O ₈ ] a anortitem Ca[Al ₂ Si ₂ O ₈ ], kde kationt Na+ je nahrazován kationtem Ca ²⁺ , je elektroneutrality dosahováno současným nahrazováním kationtu ^Si4+ kationtem ^Al3+ (jde tedy o sdruženou substituci dvojice Na ⁺ Si ⁴⁺ za dvojici Ca ²⁺ Al ³⁺ ). Obdobně ve struktuře diopsidu CaMg[Si ₂ O ₆ ] dochází k zastupování kationtu Mg ²⁺ kationtem Al ³⁺ za současného nahrazování Si ⁴⁺ kationtem Al ³⁺ (jde o sdruženou substituci, kterou vyjadřuje schéma Mg ²⁺ Si ⁴⁺ <==> 2Al ³⁺ ).

Pokud se náboje iontů s obdobnými iontovými poloměry liší více než o jednotku, je jejich zastupování v krystalové struktuře zpravidla velmi omezené nebo k němu vůbec nedochází - např. kationt U ⁴⁺ není schopen nahrazovat kationt Na ⁺ , přestože jejich iontové poloměry jsou prakticky stenné.

Na zastupování prvků ve struktuře má mj. značný vliv teplota vzniku minerálů - za jinak stejných podmínek se rozsah zastupování často zvětšuje s rostoucí teplotou. Jestliže při vysoké teplotě se mohou např. prvky „A“ a „B“ v pevném roztoku zastupovat ve zcela libovolných poměrech, může být při nižších teplotách možnost jejich vzájemného zastupování omezena a pevný roztok tvořený prvky „A“ a „B“ se tak může stát nestabilním. Takový pevný roztok se může zvolna rozpadnout na dvě samostatné fáze, z nichž jedna bude bohatší na prvek „A“ a druhá na prvek „B“. Tento proces se označuje jako rozpad pevného roztoku. K rozpadu pevných roztoků dochází např. u alkalických živců: Při vysokých teplotách se v alkalických živcích neomezeně zastupuje sodík a draslík, takže existuje souvislá řada homogenních fází od „čistého“ draselného živce o složení K[AlSi ₃ O ₈ ] přes alkalický živec o složení (K,Na)[AlSi ₃ O ₈ ] s nejrůznějšími poměry mezi K a Na až po „čistý“ sodný živec o složení Na[AlSi ₃ O ₈ ]; při nižších teplotách jsou možnosti vzájemného zastupování K a Na ve struktuře alkalických živců jen velmi omezené, a tak při nízkých teplotách dochází k rozpadu sodno-draselného živce na sodný živec a draselný živec.

Zastupování různých prvků v ekvivalentních strukturních pozicích se často označuje jako izomorfní zastupování a „pevné roztoky“ jsou považovány za součást tzv. izomorfních řad (jde např. o izomorfní řadu forsterit-fayalit). Jako izomorfní příměsi se označují prvky, které nejsou uvedeny v idealizovaném chemickém vzorci minerálu, ale které se díky izomorfnímu zastupování v minerálu vyskytují v obvykle malém množství (jde např. o Fe, Mn, Cd a In ve sfaleritu nebo o Mn a Ni v olivínu). Termínem izomorfie byla původně označována schopnost sloučenin podobných chemických vlastností tvořit krystaly stejného tvaru (slovo „izomorfie“ lze přeložit jako „stejnotvarost“) a vytvářet směsné krystaly; nyní se termínu izomorfie užívá k vyjádření vzájemného zastupování prvků v krystalové struktuře.

2.5. Krystalochemické vzorce

Krystalochemické vzorce zpravidla vyjadřují počty atomů jednotlivých prvků v základní buňce nebo v jejím určitém dílu. Izomorfní zastupování určité skupiny prvků naznačujeme v krystalochemickém vzorci jejich uzavřením v kulaté závorce, přičemž u každého prvku uvádíme počet jeho atomů (obvykle na dvě desetinná místa); za touto závorkou je zpravidla uvedena suma atomů zastupujících se prvků. Na rozdíl od chemických vzorců, v nichž je naznačeno izomorfní zastupování bez uvedení počtu jednotlivých atomů, nejsou v krystalochemických vzorcích značky zastupujících se prvků odděleny čárkami. Výpočet krystalochemického vzorce se provádí z výsledku kvantitativní chemické analýzy, a to obvykle na základě určité znalosti struktury analyzovaného minerálu (např. v podrobnější učebnici systematické mineralogie zjistíme vzorec minerálu s naznačeným izomorfním zastupováním prvků).

Výsledky chemických analýz minerálů se vyjadřují v hmotnostních procentech. Při výpočtu krystalochemického vzorce je nutno tato hmotnostní procenta převést na atomové kvocienty, které udávají počet atomů jednotlivých prvků. Při výpočtu atomového kvocientu určitého prvku se obsah tohoto prvku zjištěný chemickou analýzou (v hmot. %) dělí jeho atomovou hmotností. Takto se postupuje při výpočtu krystalochemických vzorců minerálů z třídy elementů, sulfidů a halogenidů (tj. elementů a nekyslíkatých sloučenin). Postup výpočtu krystalochemického vzorce lze ukázat například na sfaleritu, tj. na minerálu, jehož idealizovaný vzorec je ZnS, avšak o němž víme, že obsahuje řadu izomorfních příměsí, z nichž nejběžnější jsou Fe, Mn, Cd, příp. In a další elementy - toto izomorfní zastupování zinku ve struktuře sfaleritu lze naznačit vzorcem (Zn,Fe,Mn,Cd,In)S. Výsledek kvantitativní chemické analýzy sfaleritu je uveden v 1. sloupci tab. 1. (Suma uvedených prvků je 100,67 %, což svědčí o určité chybě při analýze nebo o nepřesnosti použité analytické metody.) Atomové hmotnosti stanovených prvků zjistíme v literatuře (Zn=65,37, Fe=55,85, Cd=112,40, Mn=54,94 a S=32,06) a provedeme výpočet atomových kvocientů (výsledky jsou uvedeny v 2. sloupci). Nyní již známe počty atomů jednotlivých elementů v krystalochemickém vzorci a bylo by již možno tento vzorec napsat. Vidíme však, že v idealizovaném vzorci je 1 atom síry, zatímco v našem krystalochemickém vzorci by bylo 1,0197 atomu S. Je proto vhodné provést přepočet zjištěných atomových kvocientů tak, aby jejich vzájemný poměr zůstal zachován, avšak aby krystalochemický vzorec obsahoval přesně 1 atom síry. Tento přepočet provedeme tak, že hodnotu 1 (tj. požadovaný počet atomů síry) dělíme hodnotou 1,0197 (tj. vypočteným atomovým kvocientem síry). Takto získáme určitý faktor, jehož hodnota je v našem případě 0,9807. Tímto faktorem násobíme atomové kvocienty uvedené ve sloupci 2 a získáme tak nové atomové kvocienty (sloupec 3), které po zaokrouhlení na tři desetinná místa (sloupec 4) můžeme použít k sestavení krystalochemického vzorce, v němž vyjádříme i sumu atomů, jež se vzájemně zastupují. Krystalochemický vzorec analyzovaného sfaleritu je (Zn _0,957 Fe _0,061 Cd _0,005 Mn _0,002 ) _1,025 S _1,000 . (Zaokrouhlení na tři desetinná místa bylo provedeno proto, že při obvyklém zaokrouhlení na dvě desetinná místa by nebylo možno v krystalochemickém vzorci vyjádřit obsah manganu.)

	1.	2.	3.	4.
Zn	63,77	0,9755	0,9567	0,957
Fe	3,49	0,0625	0,0613	0,061
Cd	0,60	0,0053	0,0052	0,005
Mn	0,12	0,0022	0,0022	0,002
S	32,69	1,0197	1,0000	1,000

Tab. 1. Postup výpočtu krystalochemického vzorce sfaleritu

V případě kyslíkatých sloučenin jsou výsledky chemických analýz zpravidla vyjadřovány v hmotnostních procentech kysličníků jednotlivých prvků, přičemž však celkový obsah kyslíku zpravidla není stanovován. V těchto případech se při výpočtu krystalochemického vzorce nejdříve zjistí molekulární kvocienty jednotlivých kysličníků a z nich se potom odvodí atomové kvocienty jednotlivých prvků. Dále je postup v podstatě shodný s tím, jenž byl dokumentován na příkladu sfaleritu.

	1.	2.	3.	4.	5.	6.
SiO2	36,73	0,6112	1,2224	0,6112	3,0074	3,01
Al2O3	19,99	0,1961	0,5883	0,3922	1,9298	1,93
Fe2O3	0,83	0,0052	0,0156	0,0104	0,0512	0,05
FeO	33,00	0,4593	0,4593	0,4593	2,2600	2,26

f=12 : 2,4388=4,9205
Tab. 2. Postup výpočtu krystalochemického vzorce granátu

Postup výpočtu krystalochemického vzorce kyslíkaté sloučeniny lze ukázat na příkladu minerálu ze skupiny granátu. U granátů dochází k velmi rozsáhlému izomorfnímu zastupování. Obecně má vzorec granátu formu R ²⁺ ₃ R ³⁺ ₂ [SiO ₄ ] ₃ , kde R ²⁺ jsou dvojmocné kationty jako Fe ²⁺ , Mn ²⁺ , Mg ²⁺ a Ca ²⁺ a R ³⁺ jsou trojmocné kationty jako Al ³⁺ , Fe ³⁺ nebo někdy i Cr ³⁺ , příp. další. Výsledek chemické analýzy granátu je uveden v 1. sloupci tabulky 2 (jako H ₂ O ^- se uvádí ztráta vlhkosti sušením vzorku při teplotě do 105 °C, a proto při výpočtu krystalochemického vzorce H ₂ O ^- vynecháme; suma kysličníků je 99,83 %, což naznačuje, že analýza je zřejmě velmi dobrá). Z obsahu jednotlivých kysličníků vypočteme jejich molekulární kvocienty (molekulární kvocient je roven obsahu kysličníku v hmotnostních procentech dělenému molekulovou hmotností tohoto kysličníku). Z molekulárních kvocientů, jež jsou uvedeny ve sloupci 2, vypočteme kvocienty kyslíku (sloupec 3) a kvocienty kationtů (sloupec 4) - kvocient kyslíku určitého kysličníku je roven molekulárnímu kvocientu tohoto kysličníku násobenému počtem atomů kyslíku v jeho vzorci; kvocient kationtu v určitém kysličníku je analogicky roven molekulárnímu kvocientu tohoto kysličníku násobenému počtem atomů kationtu ve vzorci kysličníku (v případě dvojmocných kationtů je kvocient kyslíku roven kvocientu kationtu a ten je roven molekulárnímu kvocientu příslušného kysličníku). Součtem hodnot ve 3. sloupci tabulky zjistíme sumu kvocientů kyslíku - v našem případě je rovna 2,4388. Víme, že v obecném vzorci granátu je celkem 12 atomů kyslíku. Proto provedeme přepočet kvocientů kyslíku a kationtů tak, aby suma kvocientů kyslíku byla rovna 12 (znamená to, že kvocienty kationtů násobíme faktorem, jenž má v našem případě hodnotu 12 : 2,4388, tedy 4,9205). Kvocienty kationtů násobené tímto faktorem jsou uvedeny ve sloupci 5. Údaje ve sloupci 5 zaokrouhlíme na dvě desetinná místa (sloupec 6) a můžeme sestavit krystalochemický vzorec, v němž v souladu s obecným vzorcem granátu sloučíme do jedné skupiny dvojmocné kationty a do druhé skupiny trojmocné kationty:

(Fe ²⁺ _2,26 Mn _0,47 Mg _0,24 Ca _0,04 ) _3,01 (A _l1,93 Fe ³⁺ _0,05 ) _1,98 [Si _3,01 O _12,00 ]

2.6. Polymorfie a polytypie

Polymorfie je schopnost určitého prvku nebo sloučeniny vytvářet odlišné krystalové struktury, označované jako modifikace. Polymorfie u prvků se někdy označuje termínem alotropie a odlišné krystalové struktury téhož prvku se pak nazývají alotropické modifikace.

Příkladem polymorfie u prvků (alotropie) jsou tři v přírodě se vyskytující modifikace síry, z nichž jedna je rombická a dvě jsou monoklinické, nebo dvě modifikace uhlíku - trigonální grafit a kubický diamant. (Dvojice grafit a diamant je známým dokladem toho, jak fyzikální vlastnosti téže látky závisejí na její krystalové struktuře.) V podobě dvou modifikací je v přírodě rozšířen CaCO ₃ (jde o trigonální kalcit a rombický aragonit) a FeS ₂ (kubický pyrit a rombický markazit). V podobě tří modifikací se vyskytuje např. Al ₂ SiO ₅ (jde o triklinický kyanit, rombický andalusit a rovněž rombický sillimanit).

Jednotlivé modifikace téže látky vznikají za různých termodynamických podmínek a každá z modifikací je stabilní v určitém intervalu teplot a tlaků. Při změně termodynamických podmínek mimo oblast stability určité modifikace se tato modifikace stává nestabilní a může dojít k fázovému přechodu, při němž změnou krystalové struktury se nestabilní modifikace mění v jinou, za daných termodynamických podmínek stabilní modifikaci. Některé fázové přechody probíhají relativně rychle, jiné velmi pomalu (přeměna probíhá několik desítek nebo stovek milionů let) a k některým fázovým přeměnám nedojde vůbec.

Speciálním případem polymorfie je polytypie. Prvek nebo sloučenina je polytypická, vyskytuje-li se v několika modifikacích, které jsou budovány strukturně a chemicky víceméně shodnými vrstvami, přičemž jednotlivé modifikace se liší jen způsobem uložení vrstev. K polytypii dochází např. u muskovitu, sfaleritu, molybdenitu a pyrhotinu.

Autor je pedagogem Katedry geologie PřF UP v Olomouci.